Co je siteswapová notace?
Občas s kamarády probíráme různé žonglérské triky/vzory. Protože se poměrně dost zaměřujeme právě na siteswapové žonglování (postavené na žonglování podle sekvencí čísel a jiných symbolů), bombardujeme se navzájem různými číselnými sekvencemi. Zvláště při jízdě v některém z prostředků hromadné dopravy tak vznikají docela komické situace. Nevím zda v tom spolucestující vidí pubertální zábavu či si myslí, že cestují s bandou autistů, každopádně jejich výrazy napovídají, že netuší co se děje. Nicméně pokud se vám podařilo vícekrát zacyklit 97531 nebo zažonglovat třeba 555559449334455555 tak to prostě chcete s ostatními probrat. Trocha zdravé soutěživosti nikdy neuškodí. Co takové sekvence čísel vyjadřují a proč je používat? Protože daný trik/vzor zvládnete popsat vašemu kamarádovi velmi přesně (za předpokladu, že siteswapové notaci rozumí). Jazyk siteswapů je též jazykem žonglérských simulátorů a pokud chcete, aby vám ukázal nějaký žonglérský trik/vzor, budete se muset naučit hovořit jako on. Další úžasnou výhodou sekvence čísel je rychlost s jakou můžete daný trik/vzor předat.
Přeložme si schválně sekvenci 555559449334455555 ze siteswapštiny do lidské řeči. Pokud tato sekvence čísel představuje vanilkový siteswap, tak znamená: "Žonglér vyhazuje s pěti míčky. Vyhazování zahájí pravou rukou a začne pěti hody kaskády. Pokračuje velmi vysokým šikmým výhozem z levé ruky. Pak vyhodí poměrně nízký hod z pravačky přímo vzhůru a pak z levačky další nízký výhoz přímo vzhůru. Pak vyhodí další velmi vysoký hod křížem, tentokrát z pravačky. Pak vyhodí z levé a hned na to z pravé dosud nejnižší výhozy křížem. Následuje výhoz přímo vzhůru levačkou a výhoz přímo vzhůru pravačkou, pak chyt prvního míčku dopadajícího z velké výšky a návrat do kaskády, do které dopadne ve vhodné chvíli druhý vysoko vyhozený míček". Myslím že z množství popsaného textu je přínos siteswapového zápisu naprosto zřejmý. Neumíte-li si představit, jak tento trik/vzor vypadá, zadejte tuto sekvenci čísel do kolonky pattern žonglérského simulátoru, zmáčkněte tlačítko juggle a hned budete moudřejší.
Možná jste teď nabyli dojmu, že siteswapová notace se týká jen pokročilých žonglérů. Není to tak uplně pravda. Její krásu sice opravdu oceníte až u komplikovanějších triků/vzorů, ale i se třemi (a dokonce i dvěma) míčky už existuje spousta zajímavých siteswapů – z toho některé jsou opravdu velmi obtížné. Jen namátkou můžete v simulátoru vyzkoušet tyto třímíčkové siteswapy "3", "42", "423", "441", "531", "51234", "60". Doufám, že jsem si touto demonstrací možností siteswapové notace získal vaši pozornost, a že se můžeme ponořit trochu hlouběji do teorie.
Velmi nepřesný rychlokurz v patnácti bodech určený těm, kteří se nechtějí zatěžovat teorií:
- Čím vyšší číslo, tím vyšší výhoz představuje.
- Lichá čísla představují výhozy jdoucí do druhé ruky tedy šikmo do kříže.
- Sudá čísla představují výhozy jdoucí do stejné ruky tedy přímo vzhůru.
- Číslo „0“ představuje prázdnou ruku na jednu dobu.
- Číslo „1“ představuje velmi nízký hod nebo podání do druhé ruky.
- Číslo „2“ představuje velmi nízký hod do stejné ruky nebo pouze držení na jednu dobu.
- Číslo „3“ představuje nízký hod do druhé ruky tak jako v kaskádě se třemi míčky.
- Číslo „4“ představuje hod do stejné ruky tak jako ve fontáně se čtyřmi míčky.
- Číslo „5“ představuje hod do druhé ruky jako v kaskádě s pěti míčky.
atd. - Do hranatých závorek se uzavírají hodnoty představující hody současně ze stejné ruky.
- Do kulatých závorek – a čísla jsou navíc odděleny čárkou – se uzavírají hodnoty představující současné výhozy z obou ruk.
- Písmeno „x“, které následuje za sudou hodnotou představuje výhoz do obvyklé výšky pro danou hodnotu ale do kříže.
- Písmeno „s“ a někdy taktéž „x“, které následuje za lichou hodnotou představuje výhoz do obvyklé výšky pro danou hodnotu ale přímo vzhůru.
- Hvězdička „*“ následující po polovině synchronního vzoru vyjadřuje „opakuj vše pro druhou stranu“. Například vzor „(6x,4)(4,6x)“ lze tak zapsat pouze jako „(6x,4)*“.
- Spočte-li se průměr z čísel siteswapové sekvence pak odpovídá počtu míčků, se kterými se žongluje. Nevýde-li celé číslo trik/vzor nelze žonglovat.
Exaktněji pojaté pojednání o siteswapové notaci
Siteswapová notace je forma zápisu umožňující zaznamenat klíčové prvky žonglérského triku/ vzoru, pomocí čísel a symbolů, v pořadí, v jakém se s objekty žongluje. Jak mocná je tato metoda dokládá ohromný pokrok od doby jejího objevení, které představovalo revoluci - neboť se najednou objevilo spoustu netušených nový triků/vzorů. „Site“ [sajt] znamená „místo“ a „swap“ [swop] znamená „vyměnit“. Siteswap tedy popisuje, jakým způsobem si místa vyměňují žonglované objekty, respektive jak si žonglované objekty vyměňují žonglující místa (obvykle jsou těmito objekty míčky a místy se obvykle myslí žonglérovi ruce). Siteswapy se primárně užívají pro vyhazovací žonglování - nejčastěji s míčky, kužely nebo kruhy - v angličtině označovaném jako „toss juggling“, nicméně existují siteswapové notace i pro žonglování do výšky s více diaboly.
Definice Siteswapu: „Pokud žonglovaný objekt mění místo způsobem určeným siteswapovou hodnotou X, znamená to, že ten samý objekt znovu změní místo o X změn později.“
I když "místem" nejčastěji bývá žonglérova ruka, může jím být libovolné jiné místo - noha, krk, odkládací plocha na skříni, ruka žonglérova kolegy, souřadnice v prostoru, špička nosu, kapsa u saka, žlutý terčík uprostřed minového pole - záleží pouze na fantazii žongléra, případně na uskutečnitelnosti výměny míst, pokud má být siteswap s užitím daných míst realizovatelný a ne pouze teoretický. Objektem bývá nejčastěji míček, ten ostatně bývá často užíván v literatuře při snahách o definici siteswapu. Může to být ale libovolný objekt, který může měnit místo - např. třicetitunový kamion. Změnou místa se obvykle myslí výhoz a následný dopad, ale může to být jakákoli akce vedoucí k tomu, že objekt své místo změní, tedy odpálení pálkou, vykopnutí, vystřelení, telekinetické přenesení objektu, teleportace. Siteswapy nemají žádné omezení, které přímo nevyplývá z definice. V dalším textu nebude-li explicitně specifikováno jinak, budeme za změnu místa považovat vyhození a následný dopad, objektem bude míček a místem bude žonglérova ruka. Výhoz objektu odpovídající siteswapové hodnotě X, může být pro jednoduchost nahrazen vyjádřením „X-ový hod“.
Definice nijak neomezuje počet žonglovaných míčků, také nespecifikuje kolik času uběhne mezi jednotlivými výhozy - přesto se hovoří o dobách nebo taktech a výškách ve smyslu: „Takto vysoký hod je přibližně devítka“. Toto zjednodušení je velmi užitečné, není ale součástí definice, a nemusí být za všech podmínek pravdivé. Můžeme ale říci, že pokud uvažujeme siteswapy za běžných předpokladů a v případě tzv. vanilkového siteswapu (tedy místy jsou ruce jednoho žongléra, který má dvě ruce, který vyhazuje míčky do vzduchu, na naší planetě, má sílu běžnou pro člověka, má běžné míčky na které působí gravitace, atd.), pak z definice do jisté míry tyto závěry vyplývají, neboť vyhodí-li žonglér míček do vzduchu, tak má na další akci čas pouze než vyhozený míček dopadne. Výšky dané zjednodušením jsou poměrné. Definice říká, že devítka je hod který bude opět vyhozen po osmi jiných hodech - musí být tedy dost vysoký na to, aby bylo možné realizovat osm jiných hodů dříve, než je objekt vyhozený „devítkovým hodem“ opět vyhozen. Je-li ale těchto osm hodů sníženo, může být i „devítka“ mnohem nižší. Výšky jsou tedy relativní vůči výškám jiných hodů a pro jeden osamocený hod se výška nedá určit vůbec - jistě ale platí, že v jednom vzoru je např. „osmičkový hod“ nižší než „hod devítkový“. Z předchozího tedy plyne, že lze siteswapovým hodnotám přiřadit i výšky v metrech, které jsou pro většinu žonglérů obvyklé.
Dále platí to, že pokud vyhozený míček není po dopadnutí do ruky znovu vyhozen (tedy například poslední hod v žonglérově životě, nebo hod, při kterém míček prostě nechtěně spadne na zem takovým způsobem, aby to mělo za následek ukončení žonglované sekvence, pak tento hod nemá žádnou hodnotu siteswapu.
Vanilkový siteswap (VSS)
Siteswapová notace byla vynalezena ve své nejjednodušší podobě známé jako „vanilla siteswap“ v roce 1985 třemi nezávislými skupinami lidí: California Institute of Technology - Bruce "Boppo" Tiemann; Santa Cruz, California - Paul Klimek; Cambridge, England - Mike Day, Colin Wright a Adam Chalcraft.[1] VSS je nejjednodušší formou SS notace, která se používá k popisu žonglérksých triků/vzorů za běžných předpokladů (uvedených výše) a navíc pouze pro asynchronní žonglování (ruce se při vyhazování střídají) a každým hodem je vždy vyhozen pouze jeden míček. Čas během kterého žonglování probíhá, dělíme ve VSS na doby (takty) určené jednotlivými výhozy. Doby se střídají pro pravou a levou ruku - tedy v první době vyhodí pravá ruka, v druhé levá, v třetí pravá, ve čtvrté levá atd.
Z definice siteswapu uvedené výše se pro dané předpoklady a omezení dá odvodit, jak budou vypadat jednotlivé hody ve VSS:
SS hodnotu 1 bude mít hod, který bude znovu vyhozen prvním dalším výhozem druhou rukou tedy o jednu dobu (takt) později - musí se tedy z jedné do druhé ruky dostat tak rychle, aby byl ihned připraven k vyhození. Můžeme tedy velmi nepřesně říci, že: „siteswapová hodnota 1 (jedničkový hod) je velmi rychlý nízký hod, nebo pouhé podání do druhé ruky“, musíme si ale uvědomit, kolik omezovacích podmínek jsme museli stanovit, abychom takovéto tvrzení mohli z definice SS odvodit, a především to, že pokud míček není po tomto velmi rychlém nízkém hodu opět vyhozen, že se pak jedná o tvrzení zcela v rozporu s definicí SS).
SS hodnotu 2 bude mít hod který, bude znovu vyhozen o dvě doby později, tedy opět stejnou rukou. Míček je tedy vyhozen jen minimálně (nebo dokonce může být vyhozen do nulové výšky - tedy nemusí být vyhozen vůbec) a dopadá do stejné ruky. Často se dvojkové hody realizují jako malé vyhození a následné chycení do klepet. Pokud bychom nebyli omezeni podmínkou pro VSS vyžadující aby místy byly právě dvě ruce, a uvažovali bychom třetí místo (například ruku žonglérova kolegy), a ruce by vyhazovaly stejným způsobem jako v případě VSS (tedy první dobu první ruka, druhou dobu druhá ruka, třetí dobu třetí ruka, čtvrtou dobu znovu první ruka atd.) potom by dvojkový hod byl hod šikmo do třetí ruky a nikoli malé vyhození vzhůru (popř. držení míčku) – jinak řečeno pro jiný počet rukou (míst), by siteswapové hodnoty odpovídaly úplně jiným výhozům.
SS hodnotu 3 bude mít hod, který bude znovu vyhozen o tři doby později, tedy nevysoký hod (ale vyšší než jedničkový) jdoucí do druhé ruky. Trojkovými hody se obvykle popisuje základního triku/vzoru se třemi míčky (kaskády se třemi míčky). Kaskádu se třemi míčky je ovšem možné pomocí siteswapů zapsat nekonečným počtem způsobů například: „3“, „522“, „72222“. Zápis ve formě „3“ je ale nejjednodušší. SS hodnotě 4 bude odpovídat hod, který bude znovu vyhozen o čtyři doby později, je to tedy v případě VSS rovný hod vzhůru, pomocí čtyřkových hodů bývá obvykle popisován základní trik se čtyřmi míčky (fontána se čtyřmi míčky).
Význam dalších čísel je možné odvodit stejným způsobem. Pro VSS platí, že míčky vyhozené s lichou hodnotou SS jsou vždy příště vyhozeny druhou rukou, a se sudou hodnotou jsou vždy příště vyhozeny stejnou rukou. Aby se toto dalo uskutečnit musí liché hody být vyhozeny tak, aby dopadly do druhé ruky a sudé do stejné ruky. Siteswapové hodnoty se zapisují postupně, tak jak jsou skutečně v triku/vzoru realizovány. Zapisuje se nejkratší opakující se sekvence čísel, je možné vytvořit dlouhou sekvenci čísel, která nemá žádnou opakující se část, v takovém případě by ale mělo být možné tuto sekvenci znovu opakovat, protože kdyby tomu tak nebylo, pak by poslední hody nebyly opět vyhozeny a neměly tudíž žádnou SS hodnotu. Pokud žonglér vyhazuje např. „...153153153153...“ zapisuje se takový trik správně jako „531“. Stejný trik, by se dal zapsat též jako „315“ nebo „153“, domluvou bylo však stanoveno, začít zápis nejvyšším číslem. Pokud je v siteswapové sekvenci více čísel stejné nejvyšší hodnoty, potom se začíná takovým, po kterém následuje nejvyšší nižší číslo atd. Pokud je možné do SS sekvence vstoupit ze základního triku (kaskády nebo fontány) pouze jediným způsobem (odpovídajícím jediné SS hodnotě) z dané sekvence čísel, bývá výjimečně toto pravidlo vědomě žongléry porušováno, například o SS „615“ se častěji hovoří jako o „561“.
Siteswapové hodnoty odpovídajícím vyšším hodům (než devítkovému) jejichž zápis vyžaduje více cifer než jednu, můžeme zapisovat oddělené čárkou, nebo používat malá písmena (např. SS se sedmi míčky, ve kterém jsou v jednu chvíli všechny míčky v přímce nad sebou, můžeme zapsat jako „13,11,97531“, ale také jako „db97531“. K ověření, zda je SS sekvence validní (zažonglovatelná) se využívá tzv. průměrovací pravidlo. Spočítáme-li průměr jednotlivých čísel SS sekvence, musí nám vyjít celé číslo, přičemž platí, že toto číslo udává počet míčků, se kterými se trik/vzor žongluje.
Např pro SS sekvenci „531“ tedy platí:
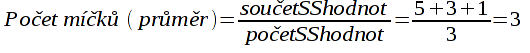
Číslo 3 je celé číslo - siteswapová sekvence „531“ je tedy z pohledu průměrovacího pravidla validní. Průměrovací pravidlo ale není jediná podmínka validity. Je také třeba dbát na to, aby se v jedné ruce nesešlo více míčků. Pokud bychom v našem příkladu změnili pořadí SS hodnot - například na „513“ - zůstane náš trik/vzor z pohledu průměrovacího pravidla stále validní, i když validní obecně není, neboť by se žonglérovi v jedné ruce sešly dva míčky. Dva míčky dopadající současně je téměř nemožné chytit, není to však problém z hlediska teorie a takový žonglérský simulátor může chytit třeba třicet míčků dopadajících současně. Teoretický problém spočívá v tom, že i kdyby žonglér dokázal chytit dva míčky dopadající ve stejnou chvíli, musel by pak vzniklou situaci řešit multiplexem (vyhozením více míčku současně z jedné ruky) to by ale bylo v rozporu se SS hodnotou, která má dle „513“ následovat, neboť sekvence „513“ s žádným multiplexem nepočítá, navíc vanilla SS (viz. omezující podmínky pro vanilla SS) vůbec multiplexy nezná.
Rozšířený siteswap (ES)
Některá omezení VSS odstraňuje obecnější forma zápisu SS - tzv. rozšířený (extended) siteswap (ES), který přidává nové možnosti. Umožňuje pracovat s více místy, vyhazovat více objektů z jednoho místa (tzv. multiplex) - v takovém případě se výhozy, které mají proběhnout současně zapisují do hranatých závorek, např. takto vypadá velmi jednoduchý příklad duplexu s pěti míčky 5555524[54]. Současně lze vyhazovat také synchronně (ruce se ve vyhazování nestřídají), jednoduchým příkladem je například synchronní fontána se šesti míčky (6,6). Občas je třeba, aby výhozy podle lichých siteswapových hodnot letěly křížem a naopak výhozy podle sudých hodnot letěli přímo vzhůru. V synchronních vzorech totiž neexistují liché hodnoty, což bylo definováno dohodou, aby si hodnoty synchronních a asynchronních vzorů odpovídaly. V synchronních vzorech vyhazují ruce současně a tak to, co v asynchronním vzoru trvá dvě doby zde trvá pouze jednu dobu. Tak by ale míček vyhozený ve fontáně se čtyřmi míčky nebyl znovu vyhozen čtvrtou ale už druhou dobou a siteswapová hodnota všech takových výhozů by byla poloviční. Neexistenci lichých křížících hodů řeší ES notace přidáním písmena „x“ vyjadřující křížení. Naopak hodu s lichou siteswapovou hodnotou lze přiřadit směr přímo vzhůru přidáním písmena „s“. Některé simulátory pro vyjádření obojího používají pouze písmeno „x“.
Všeobecný siteswap(GS)
Ani ES se bohužel nedá použít pro specifikování jiných výhozů a chytů (jako pod rukou, nohou, za zády atd.) než základních. Toto omezení odstraňuje a spoustu dalších vlastností výhozu je schopen zaznamenat až všeobecný (generalised) siteswap (GS), který vymyslel Benjamin Beever, a který používá k zápisu nikoli jen sekvenci čísel a symbolů, ale jejich matici. Tento koncept je ale popsán přímo ve zmíněné knize Návod na žonglérské vzory, na jejímž konci v dodatcích naleznete spoustu VSS, ES i GS siteswapů. Případně si můžete stáhnout siteswapové kartičky k vytisknutí a zalaminování od Gandini Juggling.
Zdroje:





